Fungsi Invers

By Posted on

Fungsi Invers – Hai sobat dosenpintar.com untuk kali ini penulis akan berbagi artikel yang disini akan membahas tentang Fungsi Invers. Bagaimana pembahasan terlengkapnya bias langsung saja sobat simak berikut dibawah ini.

Fungsi Invers
Fungsi Invers

Fungsi Invers

Fungsi invers atau dikenal sebagai fungsi kebalikan merupakan suatu fungsi yang berkebalikan dari fungsi awal atau asalnya.

Sebuah fungsi f memiliki fungsi invers (kebalikan) f-1 apabila f adalah fungsi dari satu-satu dan fungsi dalam (bijektif). Hubungan yang tersebut dapat dinyatakan seperti berikut:

(f-1)-1 = f

Simplenya, fungsi bijektif ini berlangsung ketika jumlah anggota domain sama dengan jumlah anggota pada kodomain.

Tidak ada dua atau lebih domain yang berbeda dipetakan ke kodomain sama. Serta pada setiap edaran kodomain mempunyai pasangan yang ada di domain. Perhatikan gambar di bawah ini:

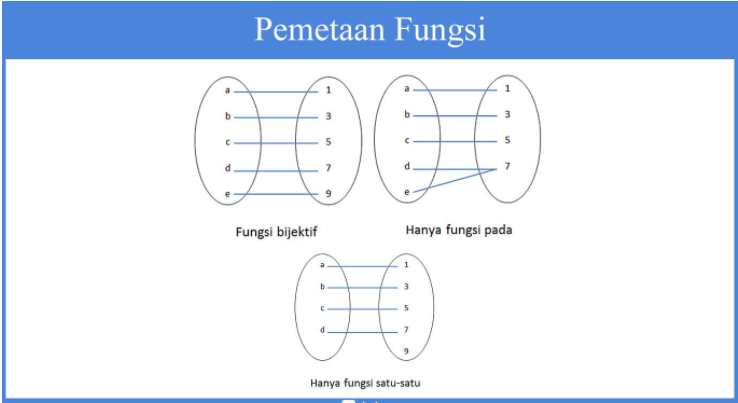
Berdasarkan gambar pemetaan pertama menunjukan sebuah fungsi yaitu fungsi bijektif. Pemetaan kedua bukan fungsi bijektif sebab pemetaan tersebut hanya berlangsung fungsi.

Invers fungsi f juga bias dinyatakan dengan f-1 seperti berikut ini:

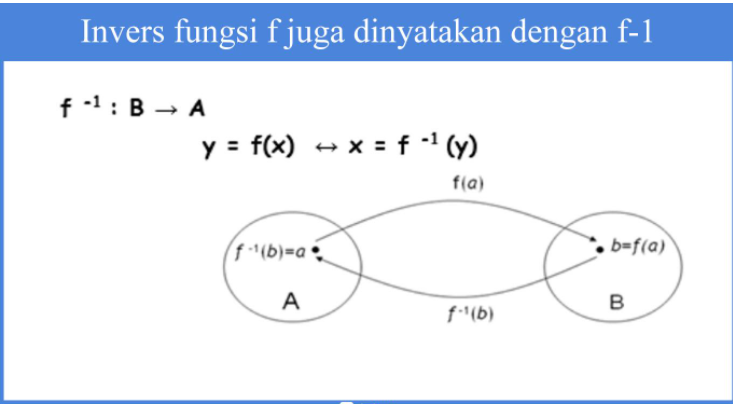
Terdapat 3 tahapan untuk menentukan fungsi invers, antara lain:

  1. Ubahlah bentuk y = f(x) kemudian menjadi bentuk x = f(y).
  2. Tuliskan x sebagai f-1(y) sehingga akan menjadi f-1(y) = f(y).
  3. Ubahlah variabel y dengan x sehingga juga akan didapatkan sebagai rumus fungsi invers f-1(x).

Dalam fungsi invers terdapat rumus khusus seperti yang ada berikut ini:

Fungsi & Komposisi

Berikut dibawah ini merupakan pembahasannya.

Aljabar Fungsi

  1. Penjumlahan f dan g

(f + g) (x) = f(x) + g(x).

Contoh Soal:

Diketahui f(x) = x + 2 dan juga g(x) = x2 – 4. Maka Tentukan (f + g)(x).

Baca Juga :  1 Kwintal Berapa Kg

Jawab:

(f + g)(x) = f(x) + gx)
(f + g)(x)= x + 2 + x2 – 4
(f + g)(x)= x2 + x – 2

  1. Pengurangan f dan g

(f – g)(x) = f(x) – g(x).

Contoh soal

Diketahui f(x) = x2 – 3x dan g(x) = 2x + 1. Tentukan (f – g)(x).

Jawab:

(f – g)(x) = f(x) – g(x)
(f – g)(x)= x2 – 3x – (2x + 1)
(f – g)(x)= x2 – 3x – 2x – 1
(f – g)(x)= x2 – 5x – 1

  1. Perkalian f dan g

(f . g)(x) = f(x) . g(x).

Contoh soal

Diketahui f(x) = x – 5 dan g(x) = x2 + x. Tentukan (f × g)(x).

Jawab:

(f × g)(x) = f(x) . g(x)
(f × g)(x)= (x – 5)(x2 + x)
(f × g)(x)= x3 + x2 – 5x2 – 5x
(f × g)(x)= x3 – 4x2 – 5x

  1. Pembagian f dan g

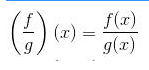
Contoh soal

Diketahui f(x) = x2 – 4 dan g(x) = x + 2. Tentukan

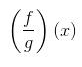
Jawab:

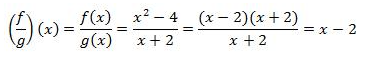
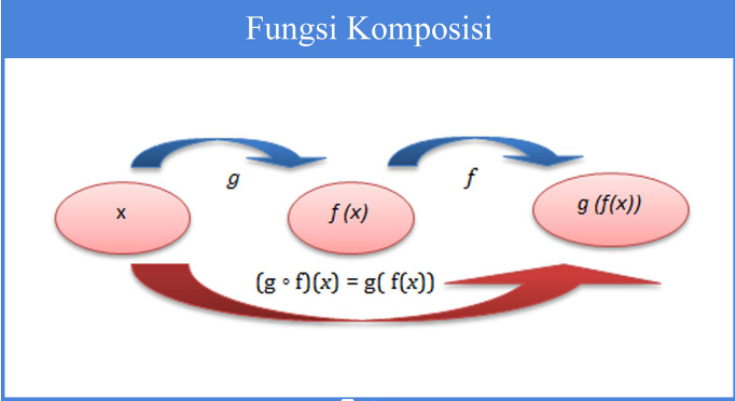
Fungsi Komposisi

Fungsi komposisi dapat tuliskan seperti berikut ini:

(f ◦ g)(x) = f (g (x))→ komposisi g (fungsi f bundaran g atau dengan fungsi komposisi dengan g yang dikerjakan terlebih dahulu daripada f)

(g ◦ f)(x)= g (f (x))→ komposisi f (fungsi g bundaran f atau dengan fungsi komposisi dengan f dikerjakan yang terlebih dahulu daripada g)

Sifat Fungsi Komposisi

  1. Tidak berlaku sebuah sifat komutatif, (f ◦ g)(x) ≠ (g ◦ f)(x).
  2. Berlaku sifat asosiatif, (f ◦(g ◦ h))(x) = ((f ◦ g)◦ h)(x).
  3. Adanya unsur identitas (l)(x), (f ◦ l)(x) = (l ◦ f)(x) = f(x).

Contoh soal:

Diketahui f(x) = 2x – 1, g(x) = x2 + 2. Maka tentukan:

  1. (g ◦ f)(x).
  2. (f ◦ g)(x).
  3. Apakah disini berlaku sifat komutatif: g ◦ f = f ◦ g?

Jawab:

  1. (g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3
  2. (f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3
  3. Tidak berlaku sifat komutatif karena g ◦ f ¹ f ◦ g.

Fungsi Invers

  1. f-1(x) adalah invers dari fungsi f(x)
Baca Juga :  1 Mil Berapa Km

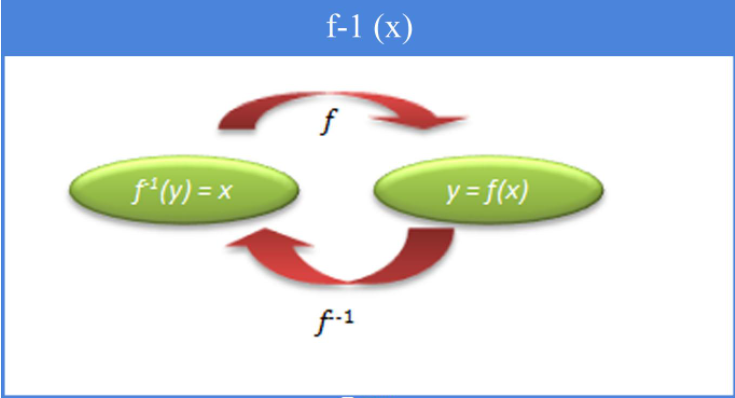
  1. Menentukan sebuah fungsi invers : mengganti f (x)= y =…” menjadi “ f-1 (y)= x = …”
  2. hubungan dari sifat fungsi invers pada fungsi komposisi:
  1. (f ◦ f-1)(x)= (f -1 ◦ f)(x)= l (x)
  2. (f ◦ g)-1 (x)= (g-1 ◦ f-1)(x)
  3. (f ◦ g)(x)= h (x)→ f (x)= (h ◦ g -1)(x)

Pembahasan soal

(SIMAK UI 2013 DASAR)

Diketahui f -1 (4x-5) = 3x-1 dan juga (f -1 ◦ f)(5)= p2 +2p – 10 maka berapa  rata-rata dari nilai p tersebut …

  1. -4
  2. -2
  3. -1
  4. 1
  5. 4

Jawab:

f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2

Menentukan nilai p

(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3

Sehingga, rata-rata nilai p yaitu

Jawabannya adalah C

(SNMPTN 2010 Dasar)

Jika g(x – 2) = 2x – 3 dan (f ◦ g)(x – 2) = 4x2 – 8x + 3, maka f(-3) =…

  1. -3
  2. 0
  3. 3
  4. 12
  5. 15

Jawab:

g(x – 2) = 2x – 3
(f ◦ g)(x – 2) = 4x2 – 8x + 3
f(g(x – 2)) = 4x2 – 8x + 3
f(2x – 3) = 4x2 – 8x + 3

Menentukan f(-3)
Jika -3 = 2x – 3 maka x = 0
Sehingga:
f(-3) = 4(0)2 – 8(0) + 3 = 3

Jawabannya: A

Demikianlah artikel mengenai pembahasan tentang Fungsi Invers. Dari pembahasan diatas semoga dapat membantu sobat dalam memahami pembelajaran mengenai fungsi invers.

Baca Juga :