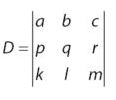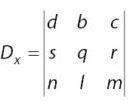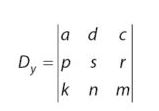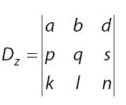Sistem Persamaan Linear Tiga Variabel (SPLTV) – Halo sobat dosenpintar.com kembali lagi penulis membagikan sebuah artikel, dan pada kesempata ini penulis akan membagikan artikel mengenai materi pembelajran matematika. Matematika itu tidak sulit jika kita paham bukan menghapal.
Nah kali ini penulis akan membahas materi mengenai tentang Sistem Persamaan Linear Tiga Variabel (SPLTV) yang meliputi Pengertian SPLTV, Definisi Dan Bentuk Umum, Menyelesaikan SPLTV Dengan Matriks, Ciri – Ciri SPLTV, Hal Yang Berkaitan dengan SPLTV, Contoh Soal Cerita SPLTV dan Contoh Soal SPLTV dan Pembahasan yang akan kita bahas satu persatu, untuk itu mari simak artikel dibawah ini hingga selesai.

Pengertian SPLTV
Daftar isi
Sistem persamaan linear tiga variabel (SPLTV) adalah sebuah persamaan matematika yang meliputi 3 persamaan linear yang masing – masing dari persamaan yang bervariabel tiga (contoh x, y dan z). Dan SPLTV juga didefinisikan sebagai suatu bentuk konsep di dalam ilmu matematika yang bermanfaat untuk menyelesaikan sebuah kasus yang tidak bisa untuk diselesaikan dengan menggunakan bentuk persamaan linear satu variabel danjuga persamaan linear dua variabel.
Definisi Dan Bentuk Umum
Sistem persamaan linear tiga variabel (SPLTV) adalah bentuk perluasan dari persamaan linear dari dua variabel (SPLDV)
Bentuk yang umum dari Sistem Persamaan Linear Tiga Variabel (SPLTV) di dalam x, y, dan juga z bisa ditulis seperti berikut ini :
ax + by + cz = d a1x + b1y + c1z = d1
ex + fy + gz = h atau a2x + b2y + c2z = d 2
ix + jy + kz = l a3x + b3y + c3z = d3
Dengan demikian ⇒ a, b, c, d, e, f, g, h, i, j, k, dan l atau a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, dan d3 = merupakan bentuk bilangan-bilangan real.
Keterangan :
- a, e, I, a1, a2, a3 = ialah bentuk koefisien dari x.
- b, f, j, b1, b2, b3 = ialah bentuk koefisien dari y.
- c, g, k, c1, c2, c3 = ialah bentuk koefisien dari z.
- d, h, i, d1, d2, d3 = ialah bentuk konstanta.
- x, y, z = ialah variabel atau peubah.
Menyelesaikan SPLTV Dengan Matriks
Menyelesaikan sistem persamaan linear dengan cara menggunakan matriks akan sangat berguna pada sistem persamaan linear dengan penggunaan variabel yang banyak, misalnya seperti pada sistem persamaan linear tiga variabel (SPLTV). Ada Metode substitusi, metode eliminasi, atau juga metode campuran dirasa kurang tepat untuk menyelesaikan SPLTV.
Apabila diketahui tiga persamaan linear dengan bentuk tiga variabel (x, y, dan z) terlihat pada persamaan seperti di bawah ini.
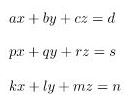
Bentuk dari SPLTV seperti di atas dalam bentuk matriks bisa dibuat seperti berikut.
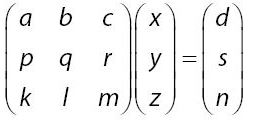
Berdasarkan bentuk matriks di atas, bisa disusun determinan yang utama, determinan bentuk variabel x, determinan dari variabel y, dan memiliki determinan variabel z. Untuk lebih jelas, maka perhatikan masing-masing bentuk determinan pada daftar yang tertera di bawah.
-
Determinan utama

-
Determinan variabel x

-
Determinan variabel y

-
Determinan variabel z

Selanjutnya jika ingin mengetahui nilai masing-masing dari variabel x, y, dan z bisa mengunakan rumus berikut ini.
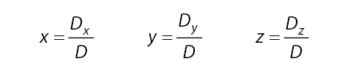
Ciri – Ciri SPLTV
Adapun ciri dari Sistem Persamaan Linear Tiga Variabel (SPLTV) juga mempunyai beberapa macam ciri – ciri tersendiri, sebagai berikut :
- SPLTV, memakai relasi tanda sama dengan (=)
- SPLTV, mempunyai tiga variabel
- SPLTV, ketiga bentuk variabel tersebut mempunyai derajat satu (berpangkat satu)
Hal Yang Berkaitan dengan SPLTV
Ada empat komponen yang berkaitan dengan SPLTV yang akan penulis uraiakn berikut ini.
-
Suku
Suku adalah bagian dari sebuah bentuk aljabar yang terdiri dari bentuk variabel, koefisien dan juga konstanta. Setiap jenis suku akan telah dipisahkan dengan bentuk tanda baca dari penjumlahan ataupun pengurangan.
Contoh :
- 6x – y + 4z + 7 = 0, maka dari itu suku – suku dari persamaan itu tersebut yaitu = 6x , -y, 4z dan juga 7.
-
Variabel
Variabel adalah pengubah atau pengganti sebuah bilangan yang biasanya bisa dilambangkan dengan memberi huruf seperti x, y dan z.
Contoh :
Doni mempunyai 2 buah rambutan, 5 buah belimbing dan 6 buah pepaya. Apabila dituliskan ke dalam bentuk dari persamaan maka hasilnya ialah :
- Misal : rambutan = x , belimbing = y dan pepaya = z, jadi persamannya adalah = 2x + 5y + 6z.
-
Koefisien
Koefisien ialah sebuan bentuk bilangan yang dapat menyatakan banyaknya sebuah jumlah variabel yang sama jenis. Koefisien bisa juga disebut dengan bilangan yang ada tepat didepan variabel, karena bentuk penulisan sebuah bentuk persamaan koefisien yang berada di depan variabel.
Contoh :
Rada mempunyai 2 buah jambu, 5 buah sawo dan 6 buah durian. Apabila ditulis ke dalam bentuk persamaan maka bentuk hasilnya adalah :
- Misal : jambu = x , sawo = y dan durian = z, sehingga mempunyai persamannya yaitu = 2x + 5y + 6z. Dari bentuk persamaan ini diketahui 2, 5 dan 6 merupakan bentuk koefisien di mana angka 2 adalah koefisien x , angka 5 adalah koefisien y dan angka 6 adalah koefisien z.
-
Konstanta
Konstanta adalah sebuah bentuk bilangan yang tidak akan diikuti dengan variabel, sehingga mempunyai nilai tetap atau konstan untuk berapapun nilai dari variabel dan peubah.
Contoh :
- 2x + 5y + 6z + 7 = 0, dari bentuk persamaan tersebut ada konstanta yaitu = 7, karena angka 7 nilainya ialah bentuk tetap dan tidak akan terpengaruh dengan berapapun bentuk variabelnya.
Contoh Soal Cerita SPLTV
Yunda mempunyai 4 buah semangka, 8 buah mangga dan 12 buah kelingking. Apabila dituliskan di dalam bentuk ke persamaan maka hasilnya adalah sebagai berikut :
Penyelesaian :
Semangka = x , Mangga = y dan Kelingking = z, sehingga bentuk persamannya yaitu = 4x + 8y + 12z.
Contoh Soal SPLTV dan Pembahasan
Nadsya mempunyai 5 buah durian, 16 buah pisang dan 20 buah sirsak. Maka jika dituliskan ke dalam bentuk sebuah persamaan maka hasilnya sebagai berikut :
Penyelesaian :
Durian = x , Pisang = y dan Sirsak = z, sehingga bentuk dari persamannya ialah = 5x + 16y + 20z.
Demikialah artikel mengenai tentang pembahasan Sistem Persamaan Linear Tiga Variabel (SPLTV) semoga bermanfaat, mohon maaf apabila terdapat kekeliruan dalam penulisan untuk itu terima kasih.
Baca Juga :