Fungsi Kuadrat – Hello para pembaca dosenpintar.com, Pada pembahasan kali ini kita akan membahas mengenai fungsi kuadrat. Dipertemuan sebelumnya kami telah membahas tentang bilangan asli dan contohnya. Kita simak langsung beserta ulasan lengkapnya di bawah ini.

Pengertian Fungsi Kuadrat
Daftar isi
Fungsi kuadrat merupakan suatu fungsi yang pangkat terbesar variabelnya adalah 2. Hampir mirip seperti persamaan kuadrat, namun berbentuk suatu fungsi. Fungsi kuadrat memiliki bentuk umum, f(x) = ax2 + bx + c = 0 dimana a, b, dan c adalah bilangan real dan a ≠ 0.
Contoh Fungsi Kuadrat
Contoh 1 :
- Diketahui : f(x) = x2 – 6x – 7
- Ditanya :
- nilai pembuat nol fungsi f
- nilai f untuk x = 0 , x = –2
- Jawab:
Nilai pembuat nol fungsi f diperoleh jika f(x) = 0
x2 – 6 x – 7 = 0
(x – 7) (x + 1) = 0
x = 7 atau x = –1
Jadi pembuat nol fungsi f adalah 7 dan –1
Untuk x = 0 maka f(0) = –7
x = –2 maka f(–2) = (–2)2 – 6 (–2) – 7 = 9
Contoh 2 :
- Tentukan nilai p agar ruas kanan f(x) = 3 x2 + (p – 1) + 3 merupakan bentuk kuadrat sempurna.
- Jawab :
Supaya merupakan suatu kuadrat sempurna, syaratnya D = 0.
D = (p – 1)2 – 4 . 3 . 3 = 0
p2 – 2p – 35 = 0
(p – 7) (p + 5) = 0
p = 7 atau p = –5
Jadi, agar ruas kanan f(x) merupakan suatu kuadrat sempurna, maka p = 7 atau p = –5.
Nilai Maksimum dan Minimum Fungsi Kuadrat
Grafik fungsi f(x) = ax2 + bx + c = 0 memiliki dua kemungkinan, yaitu terbuka ke atas atau terbuka ke bawah. Jika parabola terbuka ke atas, maka fungsi f(x) merupakan nilai minimum (Perhatikan gambar (a)). Sementara apabila parabola terbuka ke bawah, maka fungsi f(x) merupakan nilai maksimum (Perhatikan gambar (b)).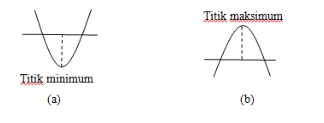
Tercapainya nilai maksimum dan nilai minimum fungsi kuadrat tergantung pada koefisien (pengali). Untuk dapat menentukan nilai maksimum/minimum fungsi kuadrat, mari perhatikan uraian berikut ini:
- f(x) = x2 – 2x – 3
= x2 – 2x + 1 – 4
=(x – 1)2 – 4
Bentuk kuadrat selalu bernilai positif atau nol, maka (x – 1)2 mempunyai nilai paling kecil (minimum) nol untuk x = 1. Dengan demikian (x – 1)2 – 4 mempunyai nilai terkecil 0 – 4 = –4.
Jadi, f(x) = x2 – 2x – 3 mempunyai nilai terkecil (minimum) –4 untuk x = 1.
Grafik/Kurva Fungsi Kuadrat
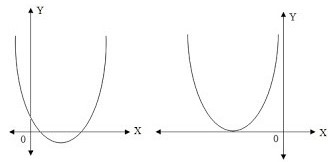
Apabila digambarkan pada koordinat Cartesius, grafik kuadrat berbentuk parabola dengan posisi parabola ditentukan oleh nilai a.
a. Jika a > 0 maka parabola terbuka ke atas
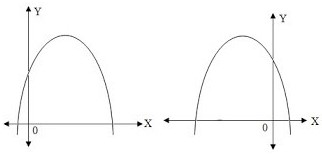
b. Jika a < 0 maka parabola terbuka ke bawah
Menentukan Fungsi Kuadrat yang Grafiknya Memenuhi Syarat-syarat Tertentu
Suatu fungsi kuadrat dapat ditentukan apabila fungsi itu:
- melalui tiga titik yang berlainan.
- memotong sumbu-X dan melalui sebuah titik lain.
- melalui sebuah titik dan koordinat titik terendah/tertinggi diketahui.
- menyinggung sumbu-X dan melalui sebuah titik.
Demikianlah artikel dosenpintar.com mengenai Fungsi Kuadrat. Semoga artikel ini bisa bermanfaat bagi anda semua
